暑期算法 第八题

题目

给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明： 每次只能向下或者向右移动一步。

输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。

输入：grid = [[1,2,3],[4,5,6]]
输出：12

来源：LeetCodeHOT100-64

题解

var minPathSum3 = function(grid) {
    const m = grid.length, n = grid[0].length

    // 状态定义：dp[i][j] 表示从 [0,0] 到 [i,j] 的最小路径和
    const dp = new Array(m).fill(0).map(() => new Array(n).fill(0))

    // 状态初始化
    dp[0][0] = grid[0][0]

    // 状态转移
    for (let i = 0; i < m ; i++) {
        for (let j = 0; j < n ; j++) {
            if (i == 0 && j != 0) {
                dp[i][j] = grid[i][j] + dp[i][j - 1]
            } else if (i != 0 && j == 0) {
                dp[i][j] = grid[i][j] + dp[i - 1][j]
            } else if (i != 0 && j != 0) {
                dp[i][j] = grid[i][j] + Math.min(dp[i - 1][j], dp[i][j - 1])
            }
        }
    }

    // 返回结果
    return dp[m - 1][n - 1]
}

题析

这又又是一道动态规划题，这次是带权规划，继续抓住三个要点：

定义数组元素的含义

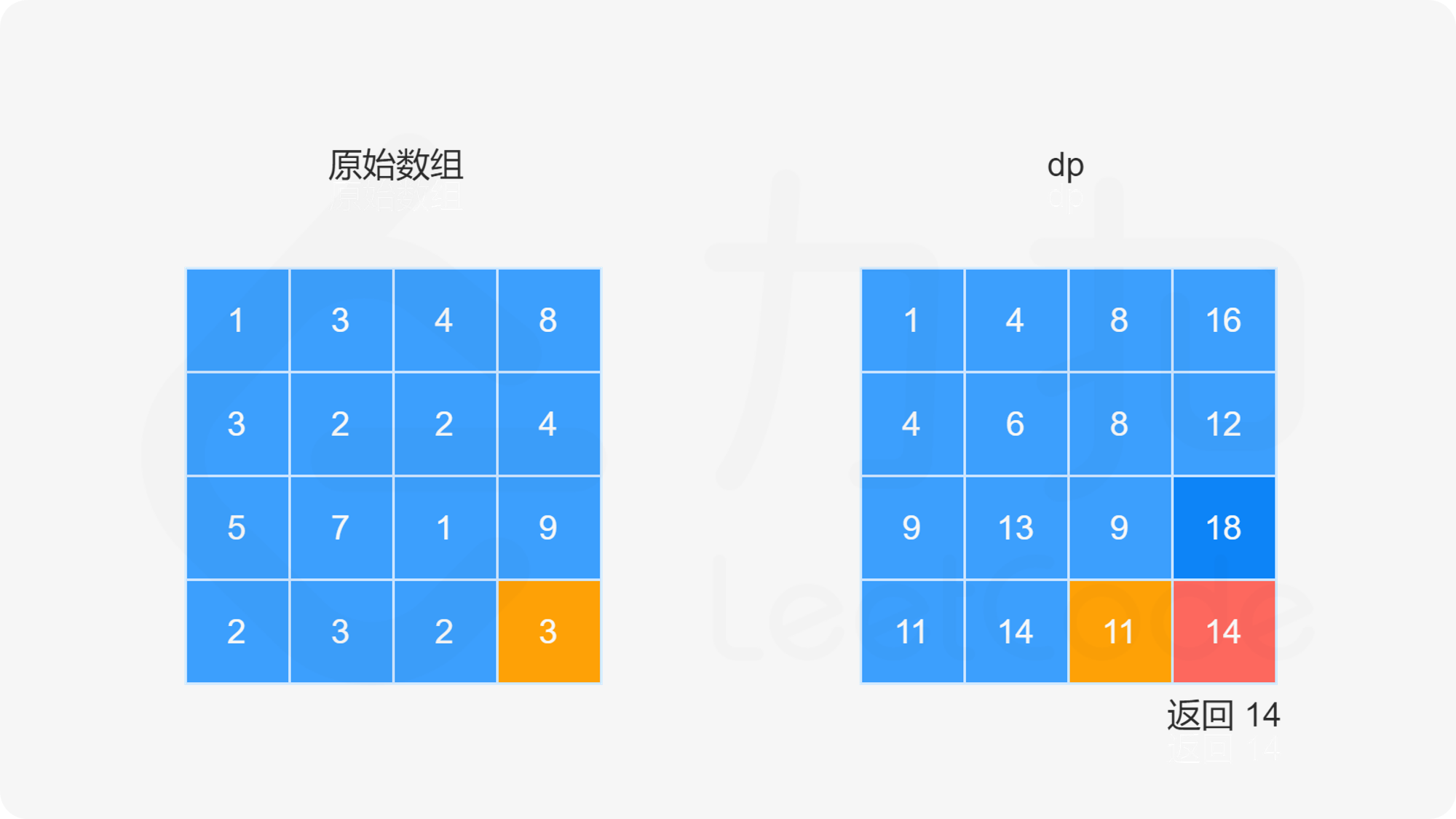
定义 dp[i][j] 的含义为：从左上角走到 (i,j) 的最小路径和。

找出数组元素间的关系式

到达(i,j)有两种方式：

• 一种是从上往下

• 一种是从左往右

每一次只选择上或左最小的路径和，所以有 dp[i，j] = min(dp[i-1][j],dp[i][j-1])+grid[i][j]。二维数组grid是权值矩阵。

找出初始条件

dp[0][0]=grid[0][0]、dp[0][j]=dp[0][j−1]+grid[0][j]、dp[i][0]=dp[i−1][0]+grid[i][0]。

题外

带权值的动态规划是很常见的题型，需要使用Min()或Max()等判断式做最佳的选择。