暑期算法 第九题
题目
给你两个单词 word1 和 word2,请你计算出将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
- 插入一个字符
- 删除一个字符
- 替换一个字符
2
3
4
5
6输入:word1 = "horse", word2 = "ros"
输出:3
解释:
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')
2
3
4
5
6
7
8输入:word1 = "intention", word2 = "execution"
输出:5
解释:
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')
来源:LeetCode-72
题解
1 | |
题析
这又又又是一道动态规划题,但比较难,仍是抓住三个要点:
定义数组元素的含义
dp[i][j] 表示以下标i-1为结尾的字符串word1,和以下标j-1为结尾的字符串word2,最近编辑距离为dp[i][j]。
有点难想象到,但逻辑是寻的通的。
找出数组元素间的关系式
1 | |
word1[i - 1] == word2[j - 1]时,即当前字符是对应相同的,所以不需要变动,dp[i][j] = dp[i - 1][j - 1],当前格子的dp等于左上角的dp,这里需要回到dp的定义,会有点难理解。可以这样看,当前字符对比相同时,需要跳过当前而对比下一个字符,word1和word2对比下一个字符就相当于dp[i + 1][j + 1],因为上一个字符相同,所以不需要操作,所以编辑距离就等于dp[i][j],由于我们需要的是下一个字符的推导式,所以可以等价于dp[i][j] = dp[i - 1][j - 1](全部变量自减1)。
word1[i - 1] != word2[j - 1]时,即当前字符是对应不同的,所以需要变动,可能是增删换其中一个。增相当于word1++,可以在矩阵中看做往下一格。增相当于word2++,可以在矩阵中看做往右一格。换相当于word1++与word2++,可以在矩阵中看做往右下一格。无论怎么操作,编辑距离都要加1。对于如何操作,自然选择最小的编辑距离。所以有dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1
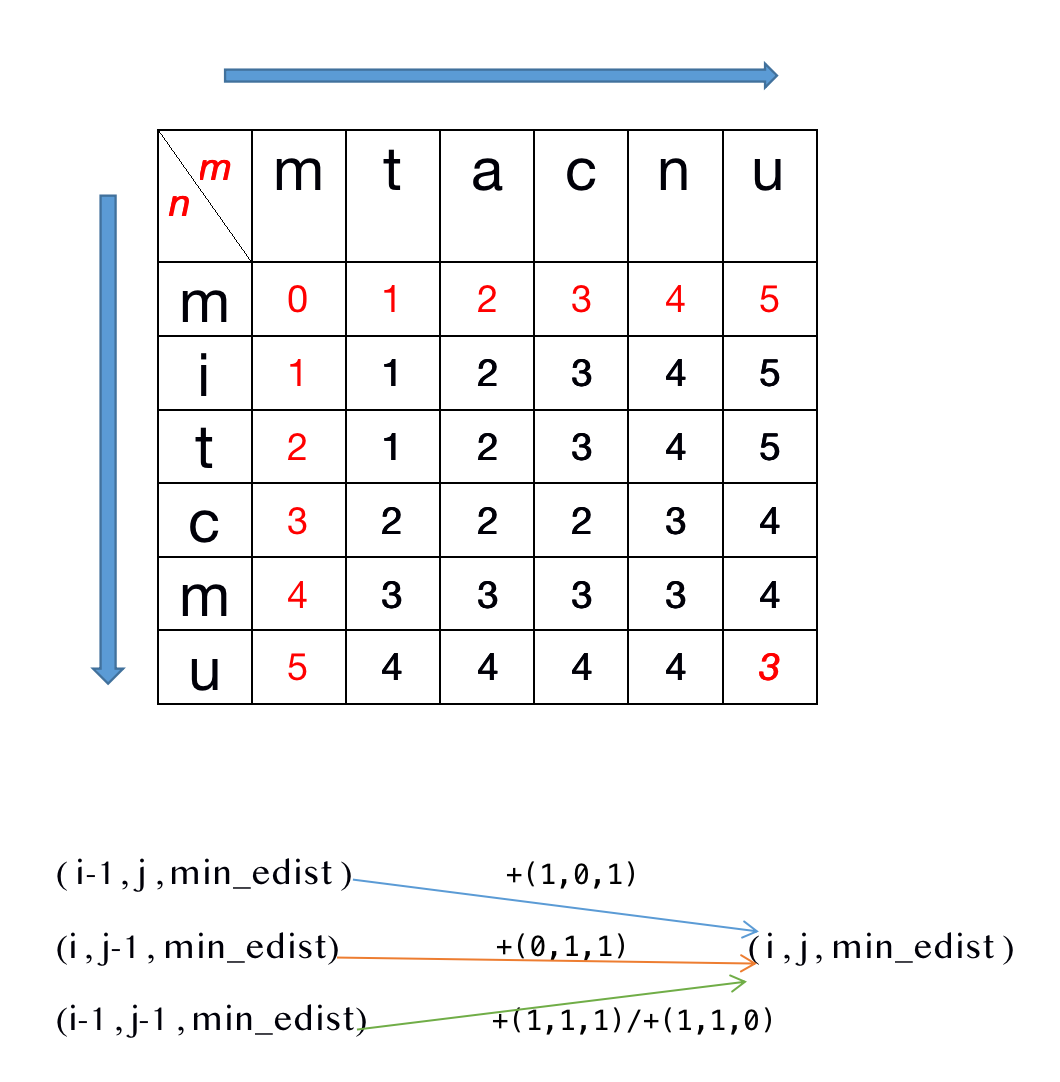
找出初始条件
dp[i][0] = i、dp[0][j] = j。
题外
dp的定义非常重要,如何定义dp仍需不断的练习。此题动态规划非常巧妙,可以多看几遍。